בעיות מתמטיות אהובות עליי

יחידות הוראה

• מבוא
  

  מבוא

  • לוח הודעות פורום

• רקע ושאלות המחקר
  

  רקע ושאלות המחקר

  פרויקט "בעיות מתמטיות אהובות עליי" הוקם בשיתוף פעולה בין מורים מובילים של רשת כיתות מופת וחוקרים של המחלקה להוראת המדעים של מכון ויצמן למדע. משתתפים רשומים בפרויקט יכולים:

  • לעיין במאגר מתפתח של בעיות מתמטיות שהוצעו על ידי משתתפי הפרויקט.
  • לדרג ולהוסיף חוות דעת על הבעיות המתמטיות במאגר.
  • להוסיף למאגר בעיות מתמטיות חדשות.
  • לדווח למשתתפי הפרויקט על התנסות בהוראת בעיות מהמאגר.

  לפרויקט ישנן מטרות פדגוגיות ומחקריות.

  מטרות פדגוגית: יצירת מאגר של בעיות מתמטיות אהובות על אנשי חינוך מתמטי שישמש משאב הוראה מתפתח, שימושי, ובאיכות גבוהה; קידום קהילה חוקרת-לומדת של מורים, מורי מורים וחוקרים אשר בוחנת בעיות מתמטיות מנקודות מבט שונות; וקידום הוראה בכיתות אשר משלבת מגוון רחב של בעיות מתמטיות הנותנות מענה לצרכים והמטרות של מורים ותלמידים שונים.

  מטרה מחקרית: לענות ביחד על השאלה הבאה, שהיא בעלת חשיבות רבה לקהילת המחקר בתחום החינוך המתמטי: "מה נחשב לבעיה מתמטית יפה/מעניינת/מאתגרת בעיניים שלנו כמורים?"

  
  

  להורדת תבנית הבעיה  |  להוספת בעיה

• מקרה פרטי של מעגל אפולוניוס בשאלת בגרות – מוצע על ידי מרים גור
  

  מקרה פרטי של מעגל אפולוניוס בשאלת בגרות – מוצע על ידי מרים גור

  
  

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה
• מינימום משקולות למקסימום טווח – מוצע על ידי יחיאל קמחי
  

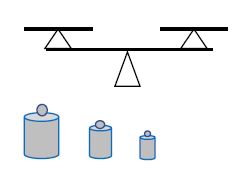
  מינימום משקולות למקסימום טווח – מוצע על ידי יחיאל קמחי

  מהו המספר המזערי של משקולות הדרוש למוכר בשוק כדי לשקול במאזניים (כמו של אלת הצדק) כל משקל בקילוגרמים שלמים מ 1Kg  ועד  40Kg ?
  

  
  

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  
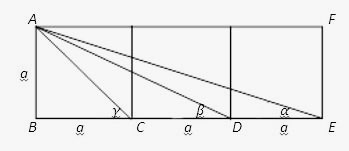
• שלוש זוויות – מוצע על ידי אלון פינטו
  

  שלוש זוויות – מוצע על ידי אלון פינטו

  המלבן בציור מורכב משלושה ריבועים זהים. הוכיחו כי .
  

  
  

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  
• מפעל שוקולד – מוצע על ידי יחיאל קמחי
  

  מפעל שוקולד – מוצע על ידי יחיאל קמחי

  ראובן ושמעון עובדים במפעל שוקולד, באריזת כדורי-שוקולד לקופסות. כל אחד משניהם קיבל ערימת כדורי-שוקולד – בכל ערימה בדיוק אתו מספר כדורים.
  הם אורזים כדורים בכל קופסה, עד למילוי הקופסה, בהתאם לנפח הקופסה.
  כל אחד מקבל קופסות בגודל אחיד, אבל הקופסות של שמעון כפולות בניפחן מקופסות ראובן.
  אם בסוף התהליך נותרים כדורים שאינם יכולים למלא קופסה, משאירים אותם בערימה.
  בסיום תהליך המילוי, נותרו בערימת ראובן 35 כדורים, ובערימת שמעון 96 כדורים.

  1. מה נפח הקופסות שמלאו שמעון וראובן?
     אנא חישבו על הפיתרון לפני שעוברים לסעיפים הבאים בשאלה.
  2. מהו המספר המזערי של הכדורים בערימה בתחילת העבודה (לפני המילוי), אם כל אחד מילא לפחות שלש (3) קופסות?
  3. מה המגבלות על מספר הכדורים כדי שמספר הפתרונים לא' יהיה:
     • 0.      אפס (0) פתרונות?
     • 1.      פתרון יחיד?
     • 2.      הרבה פתרונות שונים?
  4. כיצד משתנות התשובות לעיל אם קופסות שמעון גדולות פי שלושה/ארבעה/חמישה מקופסות ראובן?

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  

• ``איזה ספורט?`` – מוצע על ידי בוריס קויצ'ו
  

  ``איזה ספורט?`` – מוצע על ידי בוריס קויצ'ו

  איזו פעילות ספורטיבית יכולה להביא לגרף שלמטה?
  

  
  

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  
• חקר פונקציה – מוצע על ידי תמרה עוגן
  

  חקר פונקציה – מוצע על ידי תמרה עוגן

  נתונה הפונקציה:

  

  א.   מצא את תחום ההגדרה של הפונקציה f(x).

  ב.   האם הפונקציה f(x) זוגית או אי זוגית? נמק.

  ג.   השטח המוגבל ע"י גרף הפונקציה  f(x) , ציר ה-x והישרים  ו-    שווה ל-4. מצא את הערך של a .

  ד.  נתון כי הפונקציה g(x)  מקיימת:  g'(x) =f(x). אחת מנקודות החיתוך בין הגרפים של הפונקציות f(x)  ו- g(x) היא נקודה שבה x = 0 .

  (I)  הראה כי הפונקציה g(x)  מקיימת:   .   (II)   מצא את התחום שבו מתקיים:  f(x) > g(x) .

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  
• מספר ריבועי – מוצע על ידי ליליה קוט
  

  מספר ריבועי – מוצע על ידי ליליה קוט

  הוכח שהמספר

  (10ⁿ + 10^n-1 + … + 1)*(10ⁿ⁺¹ + 5) + 1

  הוא ריבוע שלם.

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  
• משושה במשולש – מוצע על ידי יעקב טובי
  

  משושה במשולש – מוצע על ידי יעקב טובי

  מאמצעי צלעותיו של משולש חד זווית העבירו אנכים לצלעות המשולש, היוצרים משושה פנימי.  הוכח כי שטח המשושה שווה למחצית שטח המשולש.
  

  
  

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  

• טריגו בלתי צפוי – מוצע על ידי ויקטוריה בולוטוב
  

  טריגו בלתי צפוי – מוצע על ידי ויקטוריה בולוטוב

  לפי מערכת משוואות לחשב את סכום:  xy+2yz+3zx

  

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  
• המרובע בר חסימה – מוצע על ידי ליליה קוט
  

  המרובע בר חסימה – מוצע על ידי ליליה קוט

  העבירו במרובע ABCD את ארבעת חוצי הזויות וקיבלו מרובע EFGH.

  • א.  הוכח: אפשר לחסום במעגל את המרובע EFGH.
  • ב.  באיזה מרובע ABCD לא יתקבל מרובע EFGH כנ"ל? נמק.

  
  

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה

  
  
• בעיית קיצון ללא אנליזה – מוצע על ידי ליליה קוט
  

  בעיית קיצון ללא אנליזה – מוצע על ידי ליליה קוט

  נתון מספר בתחום 

  באמצעותו מרכיבים שלושה מספרים נוספים:

  המספר השני הוא השורש הריבועי מהמספר הראשון.

  המספר השלישי קטן ב- 1 מהמספר השני. המספר הרביעי קטן ב- 4 מהמספר השני.

  מעלים בריבוע את המספר הרביעי, ומכפלים את התוצאה במספר השלישי.

  • מצא את המספר הראשון, שעבורו מכפלה זו היא:
    1. מינימלית
    2. מקסימלית

  חשב את ההפרש בין המכפלה המקסימלית האפשרית לבין המכפלה המינימלית האפשרית.

  
  

  פירוט הבעיה  |  חוות דעת על הבעיה